降维/排序分析（ordination analysis）

Introduction

ordination analysis（排序分析）是生态学和统计学领域中用于分析和解释多变量数据的方法之一。这个方法通常被用于探索和可视化生态学或生物学数据中的模式，尤其是在物种组成和环境因素之间的关系方面。具体可以参考张金屯老师的《数量生态学》，里面讲的非常详细，然后《数量生态学—R语言的应用》一书中还提供了所有分析的R代码，非常建议阅读。

排序分析是一种多变量分析的方法，而降维分析是其中的一部分。排序分析的目标是通过降维技术将高维数据转化为更容易理解和解释的低维形式，同时保留主要的数据结构。常见的方法包括主成分分析（Principal Component Analysis，PCA）和对应分析（Correspondence Analysis，CA）等，一般群落beta多样性分析都会用到这些方法。

排序方法根据有无解释变量可分为两种：限制性排序和非限制性排序。

限制性排序（Constrained Ordination）：这种排序方法在降维的过程中考虑了响应变量（通常是生态系统的响应，如物种组成）和解释变量（通常是环境因素）。比如冗余分析（RDA，Redundancy Analysis）就是一种限制性排序方法。
非限制性排序（Unconstrained Ordination）：这种排序方法仅仅考虑响应变量，而不考虑解释变量。比如主成分分析（PCA）是一种典型的非限制性排序方法，因为它仅关注如何最大程度地解释数据的总方差。

当涉及到排序方法时，确实有很多不同的技术，每种都有其独特的优点和应用场景。以下简要介绍常用一些方法（具体的原理和流程网上可以搜到非常多）：

常用非限制性排序

PCA (Principal Component Analysis) 主成分分析：

通过寻找数据中的主要方差方向，将高维数据转换为低维数据。主成分是原始变量的线性组合。

主成分分析（Principal Component Analysis, PCA）是一种常用的降维技术，用于分析数据集中的主要变化方向。其基本原理是通过线性变换将原始数据投影到一组新的坐标轴上，使得数据在这些新坐标轴上的方差最大。这些新的坐标轴被称为主成分。

以下是主成分分析的基本流程：

数据标准化： 如果原始数据的不同变量有不同的度量单位或变异范围，首先需要对数据进行标准化，以消除这些差异。通常，数据会被减去均值并除以标准差。
协方差矩阵计算： 对标准化后的数据计算协方差矩阵。协方差矩阵描述了不同变量之间的线性关系。
特征值分解： 对协方差矩阵进行特征值分解。特征值分解产生了一组特征值和相应的特征向量。特征值表示方差的大小，而特征向量表示对应于这些方差的方向。
选择主成分： 特征值表示主成分的重要性，通常按照特征值的大小排序。选择最大的k个特征值及其对应的特征向量，其中k是希望保留的主成分的数量。
构建投影矩阵： 将选定的特征向量构成一个投影矩阵。将原始数据乘以这个投影矩阵，即可将数据投影到新的主成分空间中。
主成分得分： 计算每个样本在新的主成分空间中的坐标，这些坐标被称为主成分得分。

PCoA (Principal Coordinates Analysis) 主坐标分析：

与PCA类似，但在距离矩阵的特征分解中使用，主坐标分析（Principal Coordinate Analysis, PCoA），也称为轴比例分析（Metric Multidimensional Scaling, MDS），是一种用于分析样本之间相似性或距离的多变量统计技术。与主成分分析（PCA）类似，PCoA旨在减少数据的维度，但它更专注于样本之间的距离或相似性而不是变量之间的协方差。

以下是主坐标分析的基本流程：

距离矩阵计算： 首先，计算样本之间的距离矩阵。这个距离可以是欧氏距离、曼哈顿距离、相关系数等，具体根据数据类型和研究问题而定，可支持的距离算法还有很多,参见?vegan::vegdist(): “manhattan”, “euclidean”, “canberra”, “clark”, “bray”, “kulczynski”, “jaccard”, “gower”, “altGower”, “morisita”, “horn”, “mountford”, “raup”, “binomial”, “chao”, “cao”, “mahalanobis”, “chisq”, “chord”, “hellinger”, “aitchison”等。。
中心化矩阵： 对距离矩阵进行中心化处理，将每个元素减去对应行和列的均值。
特征值分解： 对中心化的距离矩阵进行特征值分解。这产生了一组特征值和相应的特征向量。
选择主坐标： 选择前k个特征值及其对应的特征向量，其中k是希望保留的坐标的数量。
构建坐标矩阵： 将选定的特征向量构成一个坐标矩阵。每个样本在这些坐标上的投影就构成了主坐标。
主坐标分析图： 将样本在主坐标上的投影绘制成图表，这就是主坐标分析图。这个图表展示了样本之间的相对位置，反映了它们在多维空间中的相似性或差异。

主坐标分析通常用于分析生态学数据或其他具有样本相似性结构的数据。通过降低维度，它使得研究者更容易理解和可视化样本之间的关系。

CA (Correspondence Analysis) 对应分析：

用于分析两个或多个分类变量之间的关系，通常用于探索物种和环境因子之间的关联。

对应分析（Correspondence Analysis，简称CA）是一种用于分析两个分类变量之间关系的多元统计技术。它可以用于研究分类表格（Contingency Tables），特别是在生态学、社会学、市场调查等领域。

以下是对应分析的基本流程原理：

建立列联表： 首先，构建一个列联表，其中包含两个或更多的分类变量的频数或百分比。
计算期望频数： 对于每个单元格，计算在独立性假设下的期望频数。独立性假设是指假设两个变量之间没有关联。
计算标准化残差： 对每个单元格的实际频数和期望频数进行比较，计算标准化残差。残差表示实际观察到的频数与期望频数之间的差异，标准化残差则考虑了这种差异相对于整体表格的变异性。
奇异值分解： 对标准化残差矩阵进行奇异值分解。奇异值分解是一种矩阵分解方法，将一个矩阵分解成三个矩阵的乘积。
选择主维度： 根据奇异值的大小选择主维度。这些主维度是原始变量的线性组合，通常是用于解释数据中大部分变异的维度。
计算坐标： 计算每个变量和每个水平与垂直刻度上的坐标，这些坐标用于可视化数据。
绘制对应图： 使用计算得到的坐标信息，绘制对应图。对应图有助于理解变量之间的关系以及在数据中的结构。

总的来说，对应分析通过将多维数据映射到低维空间，提供了一个直观的方式来可视化和解释分类数据中的关联关系。

DCA (Detrended Correspondence Analysis) 去趋势对应分析：

CA的一种变体，DCA的目标是消除或减少由于群落数据中的趋势而导致的主坐标轴的拉伸。

以下是去趋势对应分析的基本流程原理：

数据标准化： 首先，对群落数据进行标准化，以确保各种生境的贡献相等。这通常包括对物种丰富度进行对数或平方根转换。
进行初始对应分析： 对标准化后的数据进行初始对应分析，计算初始的主坐标轴。
去除趋势： 通过拟合一条曲线（通常是第二主坐标轴）来去除数据中的趋势。这可以通过回归分析等方法来完成。
重新计算坐标： 在去除趋势后，重新计算主坐标轴。
绘制DCA图： 使用去趋势后的坐标信息，绘制DCA图。DCA图通常是一个双轴图，显示了样点或物种在主坐标轴上的分布。
解释结果： 根据DCA图的形状和方向，解释物种和样点之间的关系。这有助于理解群落数据的结构，而不受主坐标轴的人为拉伸的影响。

DCA的优势在于它可以更好地处理生态学数据中常见的非线性趋势。通过去除趋势，DCA提供了更为真实和可解释的关于生态群落结构的信息。

NMDS (Non-Metric Multidimensional Scaling) 非度量多维缩放：

通过样本间的距离矩阵来构建降维空间，以保持样本之间的相对距离。同样可使用各种距离算法。

以下是非度量多维缩放的基本流程原理：

计算相异性矩阵： 首先，根据数据集中的样本或物种的相异性（比如，物种组成的差异）计算相异性矩阵。这可以使用各种相异性或距离指标，如Bray-Curtis距离、Jaccard相异性等。
初始化配置： 随机或基于一些启发式算法初始化样本或物种在多维空间中的位置。
迭代寻找最佳位置： 通过迭代，调整样本或物种在多维空间中的位置，使得它们在相异性空间中的相对位置更好地匹配相异性矩阵。这通常通过最小化实际相异性矩阵和在多维空间中的拟合相异性矩阵之间的差异来实现。
停止准则： 根据一些停止准则，比如迭代次数、梯度大小等，确定算法何时停止。
输出结果： 最终的结果是样本或物种在低维空间中的坐标。
绘制NMDS图： 使用NMDS生成的坐标，可以绘制NMDS图，展示样本或物种在低维空间中的位置。

NMDS的优势在于它能够在保留样本或物种间的相异性的同时，将高维数据映射到低维空间。这有助于可视化数据中的结构，并且对于那些不能满足线性假设的数据而言是一种有用的技术。

t-SNE (t-distributed Stochastic Neighbor Embedding) t-分布随机邻域嵌入：

主要用于保留样本之间的局部相似性，常用于高维数据的可视化。

以下是t-SNE的基本流程原理：

相似性矩阵： 对于给定的高维数据集，首先计算样本之间的相似性，通常使用高斯分布来表示样本之间的相似性。这会生成一个相似性矩阵。
学习相似性： 在低维空间中，使用t-分布来表示样本之间的相似性。t-SNE尝试保持样本对之间的相似性，使得在高维空间中相似的样本在低维空间中仍然保持相似。
梯度下降： 使用梯度下降等优化算法，尝试最小化高维空间中的相似性矩阵与低维空间中的相似性分布之间的差异。这个过程会调整低维空间中的样本位置，以更好地反映它们在高维空间中的相似性。
调整参数： t-SNE有一些参数，比如困惑度（perplexity），用于调整算法的行为。困惑度控制了在生成高维空间中的相似性分布时每个样本可以考虑多少个邻近样本。
迭代： t-SNE是一个迭代过程，通过多次迭代来优化低维表示，直到满足停止准则。
输出结果： 最终的结果是样本在低维空间中的坐标。

t-SNE广泛用于数据可视化，尤其是在深度学习中，以及在发现高维数据的结构和簇时。然而，对于大型数据集，计算成本可能较高。

UMAP (Uniform Manifold Approximation and Projection) 统一流形逼近和投影：

与t-SNE类似，用于高维数据的降维和可视化，但在某些情况下可能比t-SNE更快、更保持全局结构。

统一流形逼近和投影是一种用于学习高维数据的低维表示的方法。这一方法旨在找到一个低维流形，可以保持数据的局部结构。以下是它的基本原理：

数据表示： 假设我们有一个高维数据集，可以用$X \in \mathbb{R}^{n \times m}$ 表示，其中$n$ 是样本数，$m$ 是特征数。
流形假设： 统一流形假设认为高维数据集$X$ 实际上是嵌入在一个低维流形中的，该流形在高维空间中扭曲和弯曲。
局部保持： 统一流形逼近和投影的目标是找到一个低维表示$Y \in \mathbb{R}^{n \times k}$，其中$k$ 是目标低维度，以便在这个低维表示中，原始数据的局部结构得以保持。
数学形式： 通常，这可以通过最小化两个项的和来实现：
- 重构误差项： 衡量在低维空间中的表示$Y$ 如何能够准确地重构原始数据$X$。
- 流形保持项： 衡量$Y$ 中的点是如何在原始数据空间中保持局部结构的。
优化问题： 统一流形逼近和投影可以被建模为一个优化问题，通过调整$Y$ 来最小化重构误差和流形保持项。

这种方法的目标是在低维空间中找到一个紧凑的表示，以便原始数据集的结构得以保持。在实际应用中，这对于高维数据的可视化和特征学习非常有用。常见的统一流形逼近和投影的方法包括 t-SNE（t-Distributed Stochastic Neighbor Embedding）和UMAP（Uniform Manifold Approximation and Projection）。

分组变量排序

LDA (Linear Discriminant Analysis) 线性判别分析：

用于降低数据维度，同时最大化不同类别之间的差异，通常用于分类问题。其基本思想是将数据投影到一个低维空间中，以便在这个低维空间中更容易区分不同类别的数据点。

下面是LDA的基本流程和原理：

计算类内散度矩阵和类间散度矩阵： 对于给定的数据集，首先计算每个类别内部的散度矩阵（表示类别内部数据点的分散程度）和整个数据集的类间散度矩阵（表示不同类别之间数据点的分散程度）。
计算特征向量和特征值： 对于矩阵的逆矩阵乘以类内散度矩阵，然后计算这个结果的特征向量和特征值。通常，选择最大的特征值对应的特征向量。
选择投影方向： 将特征向量按照对应的特征值大小排序，选择前k个特征向量构成投影矩阵，其中k是新的特征空间的维度。
投影： 将原始数据集乘以投影矩阵，得到新的、低维的数据集。

LDA的目标是通过最大化类间散度和最小化类内散度，从而在降维的同时保留类别信息。由于其考虑了类别信息，因此LDA通常在分类问题中效果很好。

总体而言，LDA是一种监督学习的降维技术，与PCA（主成分分析）等无监督学习的降维方法有所不同。PCA关注的是数据整体的方差，而LDA关注的是不同类别之间的差异。

PLSDA (Partial Least Squares Discriminant Analysis) 偏最小二乘判别分析：

用于处理分类问题，特别是在多变量数据中，它将变量分解为与响应变量相关的成分。

偏最小二乘判别分析（Partial Least Squares Discriminant Analysis, PLS-DA）是一种用于处理多变量数据、进行降维和分类的方法，特别适用于高度相关的解释变量和存在分类问题的情境。

以下是PLS-DA的基本流程和原理：

选择类别： 确定数据集中的类别信息。
数据标准化： 对输入数据进行标准化，以确保不同变量的尺度相同。
初始化： 初始化权重和载荷，这些是通过对类别信息建模而优化的参数。
交替优化： 通过交替地最小化预测误差来优化权重和载荷。
计算成分： 基于最优权重和载荷，计算新的成分。这些成分是原始变量的线性组合，被用于构建新的特征。
重复步骤： 重复上述步骤，直到达到预定的成分数量或满足某个停止准则。
分类： 使用获得的成分进行分类。在PLS-DA中，通常采用阈值将样本分配给不同的类别。

PLS-DA与普通的PLS回归方法相似，但其主要目标是区分类别而不是建立回归模型。在数据有潜在结构、且类别信息存在的情况下，PLS-DA通常比传统的判别分析方法表现更好。

常用限制性排序

限制性排序方法在生态学和其他领域中经常用于研究响应变量和解释变量之间的关系。

RDA (Redundancy Analysis) 冗余分析：

简介： RDA 是一种用于解释响应变量的多变量技术，通过最大化解释响应变量的方差来找到解释变量中的线性组合。
应用： 通常用于生态学中研究物种丰富度、组成或其他响应变量与环境因子之间的关系。

以下是冗余分析的基本流程和原理：

数据收集： 收集包括响应变量（依赖变量）和预测变量（自变量）的多变量数据。
数据标准化： 对数据进行标准化，以确保不同变量的尺度相同。
构建模型： RDA基于线性模型，试图找到一个线性关系，最大程度地解释响应变量的方差。
分解方差： 将响应变量的方差分解为与预测变量直接相关的部分和不相关的部分。冗余分析的关键是找到与预测变量相关的冗余分量。
排序和解释： 对于冗余分量，可以进行排序以了解哪些预测变量对解释响应变量的变异最为重要。
检验显著性： 使用统计检验来确定模型的显著性。这包括检验模型整体的显著性以及每个预测变量对模型的个别贡献。

冗余分析的主要优势在于它可以处理多个响应变量和多个预测变量，同时考虑它们之间的相关性。这使得它在解释生态系统中多变量关系方面非常有用。

db-RDA (distance-based Redundancy Analysis) 基于距离冗余分析：

简介： db-RDA 是一种基于距离矩阵的 RDA 方法，适用于非线性和非对称关系。
应用： 适用于样本间的非线性相似性关系，比如在物种组成数据中。

基于距离的冗余分析（Distance-based Redundancy Analysis, dbRDA）是冗余分析（RDA）的一种扩展形式，主要应用于处理非欧几里得的生态数据。在传统的RDA中，数据通常被假设为多元正态分布，但这在处理生态学数据时可能不合适，特别是在存在非对称性、离群值或多重共线性等情况下。

以下是基于距离的冗余分析的基本流程和原理：

距离矩阵的计算： 首先，需要计算响应变量和预测变量之间的距离矩阵，以代替传统RDA中使用的协方差矩阵。这通常涉及到计算 Bray-Curtis 距离、Euclidean 距离或其他适用于非欧几里得空间的距离。
模型构建： 类似于传统的RDA，基于距离的冗余分析也是通过构建一个线性模型来描述响应变量和预测变量之间的关系。这个模型的目标是最大化解释响应变量的方差。
模型解释： 解释模型的冗余分量，理解每个预测变量对响应变量的贡献。这涉及到排序和解释冗余分量的过程。
检验显著性： 对模型整体和每个预测变量的显著性进行统计检验。

基于距离的冗余分析的优势在于它能够处理生态学数据的非正态性和异方差性，同时不需要假设线性关系。这使得它更具灵活性，适用于更广泛的生态学和环境数据。

CCA (Canonical Correspondence Analysis) 典型对应分析：

简介： CCA 是对应分析 (CA) 的扩展，以解释响应变量的变异性。
应用： 常用于研究生态学中物种丰富度和环境因子之间的关系。

典型对应分析（Canonical Correspondence Analysis, CCA）是一种用于分析两个表之间关系的多变量统计技术。它将两个数据表之间的行和列之间的关系通过最大化它们之间的典型相关性来建模。这个方法通常应用于生态学和环境科学，用于研究环境因素（如温度、湿度等）与物种分布之间的关系。

以下是典型对应分析的基本流程和原理：

数据准备： 收集两个表的数据，一个表包含环境变量（如温度、湿度等），另一个表包含生物群落数据（物种的存在与否、丰度等）。
计算典型变量： 使用环境变量和生物群落数据来计算典型变量。这通常涉及到将数据进行标准化和转换。
典型对应分析模型： 构建一个模型，通过最大化环境变量和生物群落数据之间的典型相关性。这个模型可视为一个对生态系统中生物群落和环境变量之间关系的描述。
解释结果： 解释模型的典型相关系数，了解环境因子如何与生物群落结构相关。通常，通过查看典型变量的负载ings（loadings）来解释环境和生物群落之间的关系。
显著性检验： 对模型整体和每个典型轴的显著性进行检验。

典型对应分析的主要目标是帮助解释生态系统中环境因素和生物群落之间的关系。它通常用于揭示环境梯度如何影响生物多样性和生态系统结构。

分析与绘图

vegan包是生态群落研究中最常用的包之一，里面包含了大部分的分析函数。

pctax包提供了快速完成各种排序分析及可视化（bi-plot，tri-plot）的函数：b_analyse用于常用非限制性排序和分组响应变量排序，myRDA, myCAP, myCCA用于常用限制性排序。

1
2
3
4
5
6


#安装pctax包
if(!requireNamespace("pctax"))remotes::install_github("Asa12138/pctax")

library(pctax)
#查看帮助
?pctax::b_analyse

b_analyse的参数也非常简单：

otutab: an otutab data.frame, samples are columns, taxs are rows. 这是我们要输入的高维响应变量数据。
norm: should normalized or not? (hellinger) 是否进行标准化，我们一般做物种丰度数据时会使用hellinger进行转化。
method: one of “pca”, “pcoa”, “ca”, “dca”, “nmds”, “plsda”, “tsne”, “umap”, “lda”, “all”，选择以下方法的一种或几种，选”all”就全部跑完。
group: if use lda or plsda, give a group vector，如果用分组响应变量排序，那就输入分组变量，注意和输入的otutab的列对应。
dist: if use pcoa or nmds, your can choose a dist method (default: euclidean)，如果用的是基于距离的pcoa和nmds，那就可以选择距离计算方法。

比如我们做一个PCA试试，产生的b_res包含4个内容：1是两个轴的解释度，2是每个样本的位置，2是每个变量的位置，4是每个变量的贡献度（不是所有方法都能计算贡献度）。

1
2


data(otutab,package = "pcutils")
head(otutab)

##                               NS1  NS2  NS3  NS4  NS5  NS6  WS1  WS2  WS3  WS4
## s__un_f__Thermomonosporaceae 1092 1920  810 1354 1064 1070 1252 1597 1330  941
## s__Pelomonas_puraquae        1962 1234 2362 2236 2903 1829  644  495 1230 1284
## s__Rhizobacter_bergeniae      588  458  889  901 1226  853  604  470 1070 1028
## s__Flavobacterium_terrae      244  234 1810  673 1445  491  318 1926 1493  995
## s__un_g__Rhizobacter         1432  412  533  759 1289  506  503  590  445  620
##                               WS5  WS6  CS1  CS2  CS3  CS4  CS5  CS6
## s__un_f__Thermomonosporaceae 1233 1011 2313 2518 1709 1975 1431 1527
## s__Pelomonas_puraquae         953  635 1305 1516  844 1128 1483 1174
## s__Rhizobacter_bergeniae      846  670 1029 1802 1002 1200 1194  762
## s__Flavobacterium_terrae      577  359 1080 1218  754  423 1032 1412
## s__un_g__Rhizobacter          657  429 1132 1447  550  583 1105  903
##  [ reached 'max' / getOption("max.print") -- omitted 1 rows ]

1

b_analyse(otutab,method = "pca")->b_res

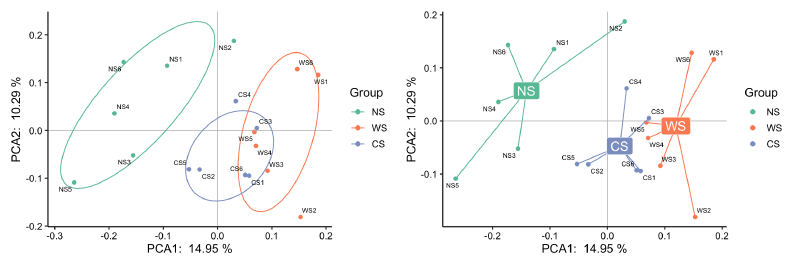
要对结果进行可视化也非常简单，直接plot就行。这里给所有的样本映射了一个分组值，metadata是包含样本分组设计和各种环境因素的表格，“Group”是metadata的一列：

1

plot(b_res,Group = "Group",metadata = metadata)

## $PCA

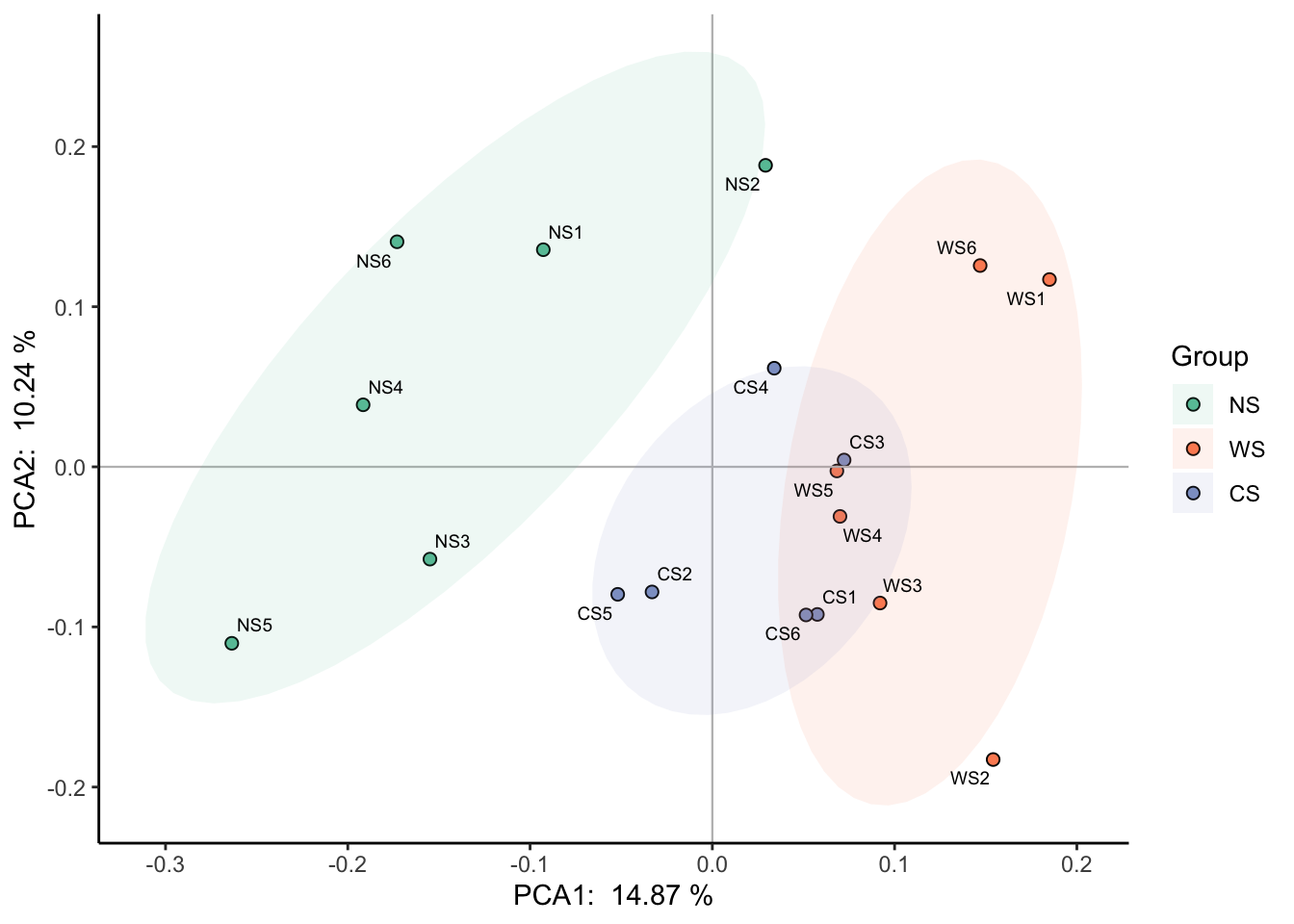
对于这种分组的显著性（怎么说明三组的群落组成存在显著差异？），具体有adonis/mrpp/anosim/mantel等方法（可参考https://blog.csdn.net/qq_42830713/article/details/129073120）,一般用vegan包的adonis2函数（又叫PERMANOVA，Permutational Multivariate Analysis of Variance Using Distance Matrices）来检验。

pctax::permanova函数也整合了几种方法，可以获得对应的R方和p值，然后标在PCA图上。注意这几种方法都是基于距离的，建议检验方法和降维方法使用的距离保持一致

1

pctax::permanova(otutab,metadata["Group"],method = "adonis")

##   group     r2 p_value  sig
## 1 Group 0.1832   0.001 TRUE

1

pctax::permanova(otutab,metadata["Group"],method = "mrpp")

##   group      r p_value  sig
## 1 Group 0.0375   0.002 TRUE

1

pctax::permanova(otutab,metadata["Group"],method = "anosim")

##   group      r p_value  sig
## 1 Group 0.3947   0.001 TRUE

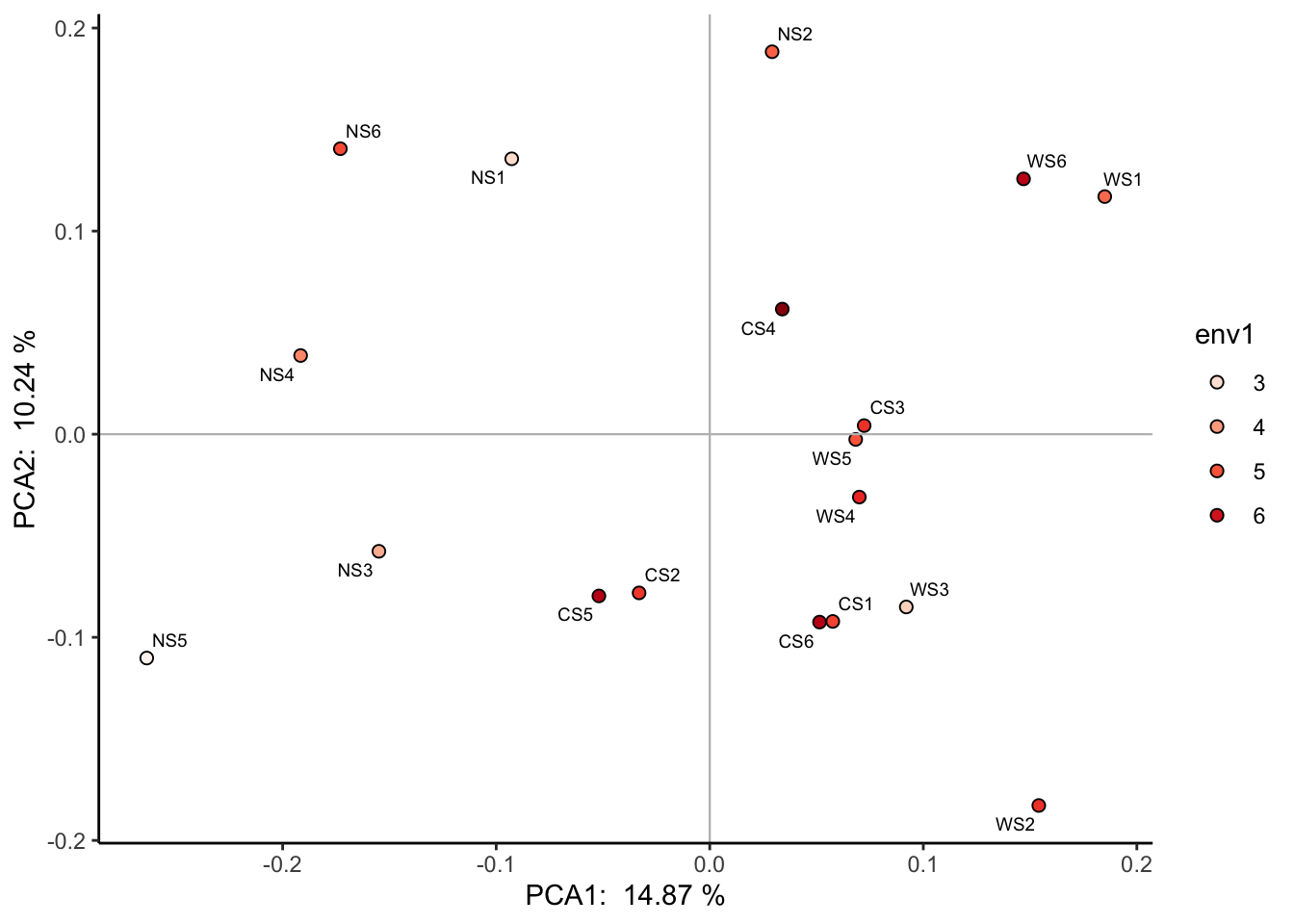
也可以将连续变量映射到颜色上：

1

plot(b_res,Group = "env1",metadata = metadata)

## $PCA

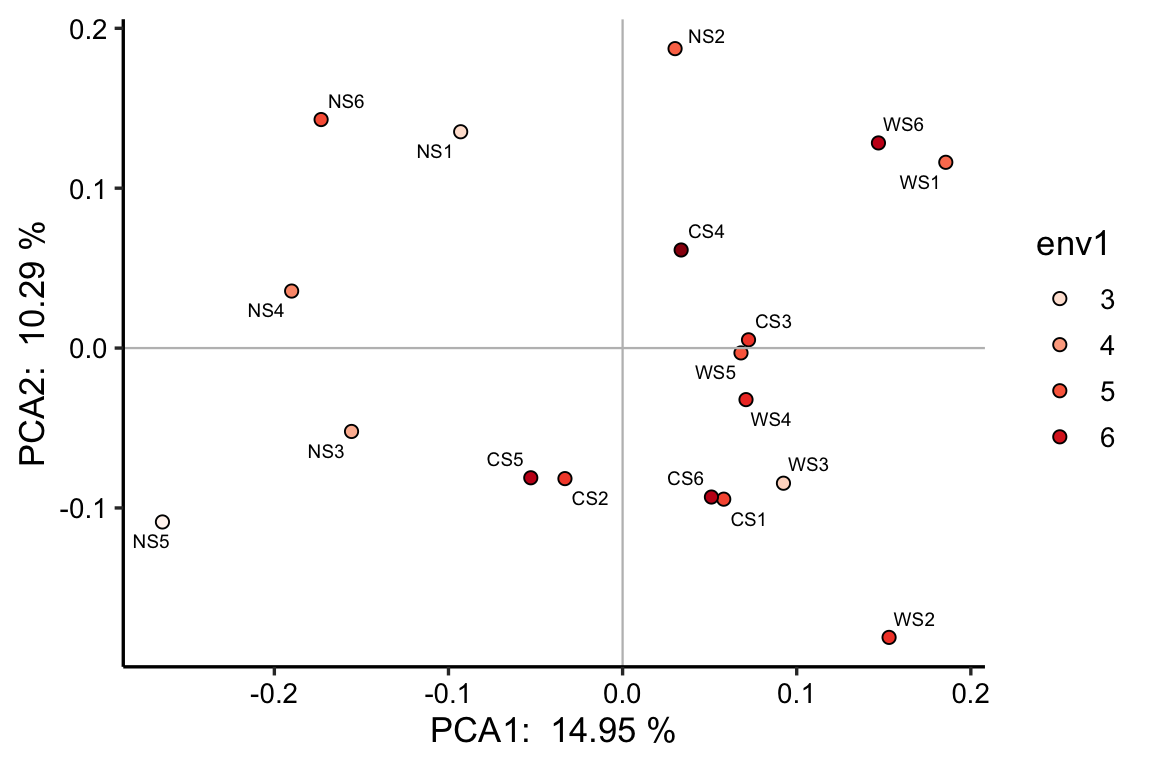
绘图有很多可以灵活调节的参数：

?pctax:::plot.b_res

mode 是绘图风格，1～3都是我常用的：

1
2


plot(b_res,Group = "Group",metadata = metadata,mode = 2)
plot(b_res,Group = "Group",metadata = metadata,mode = 3)

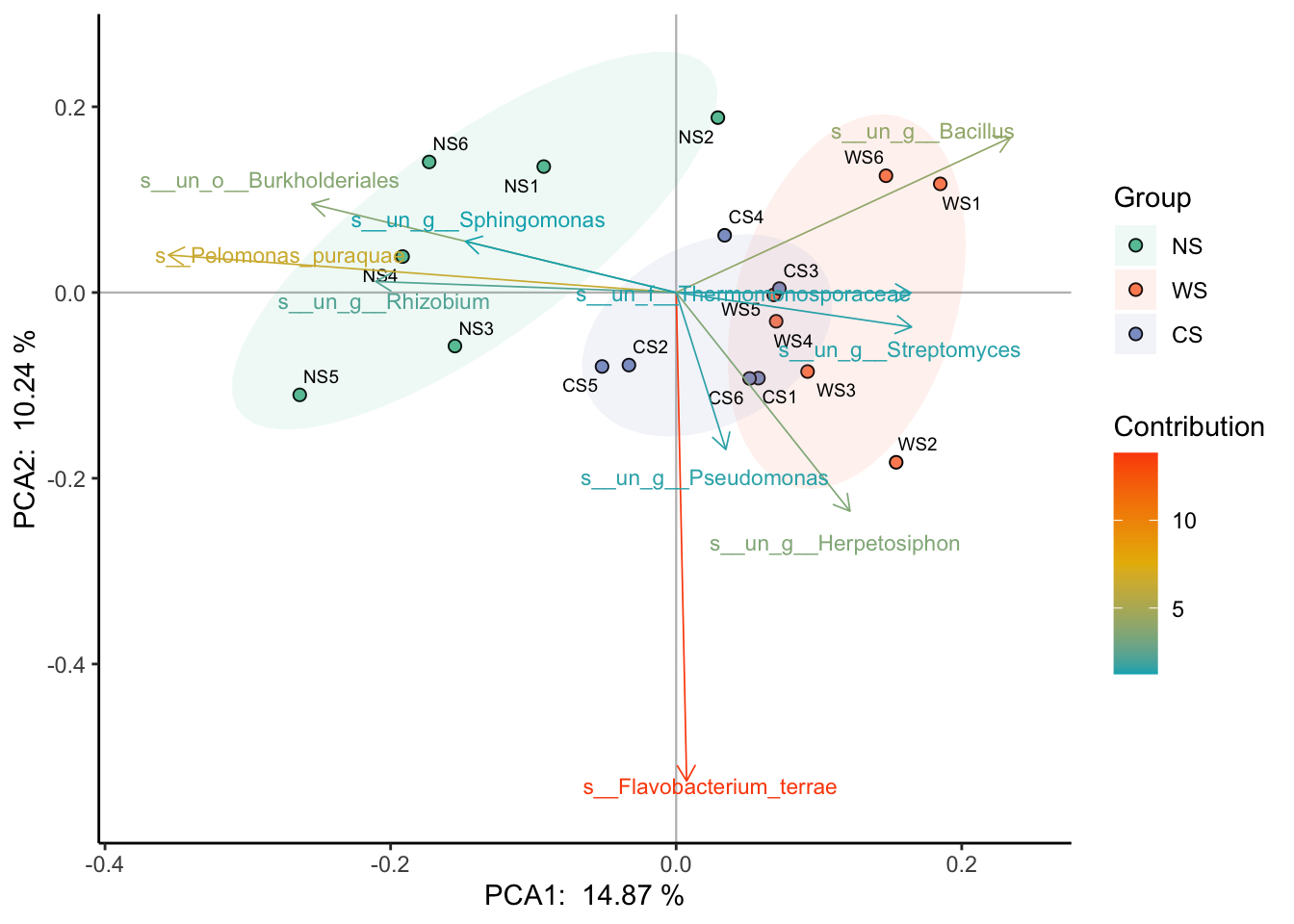
把bi设为true的话，会画出一部分贡献度最高的变量：

1

plot(b_res,Group = "Group",metadata = metadata,bi = T,Topn = 10)

## $PCA

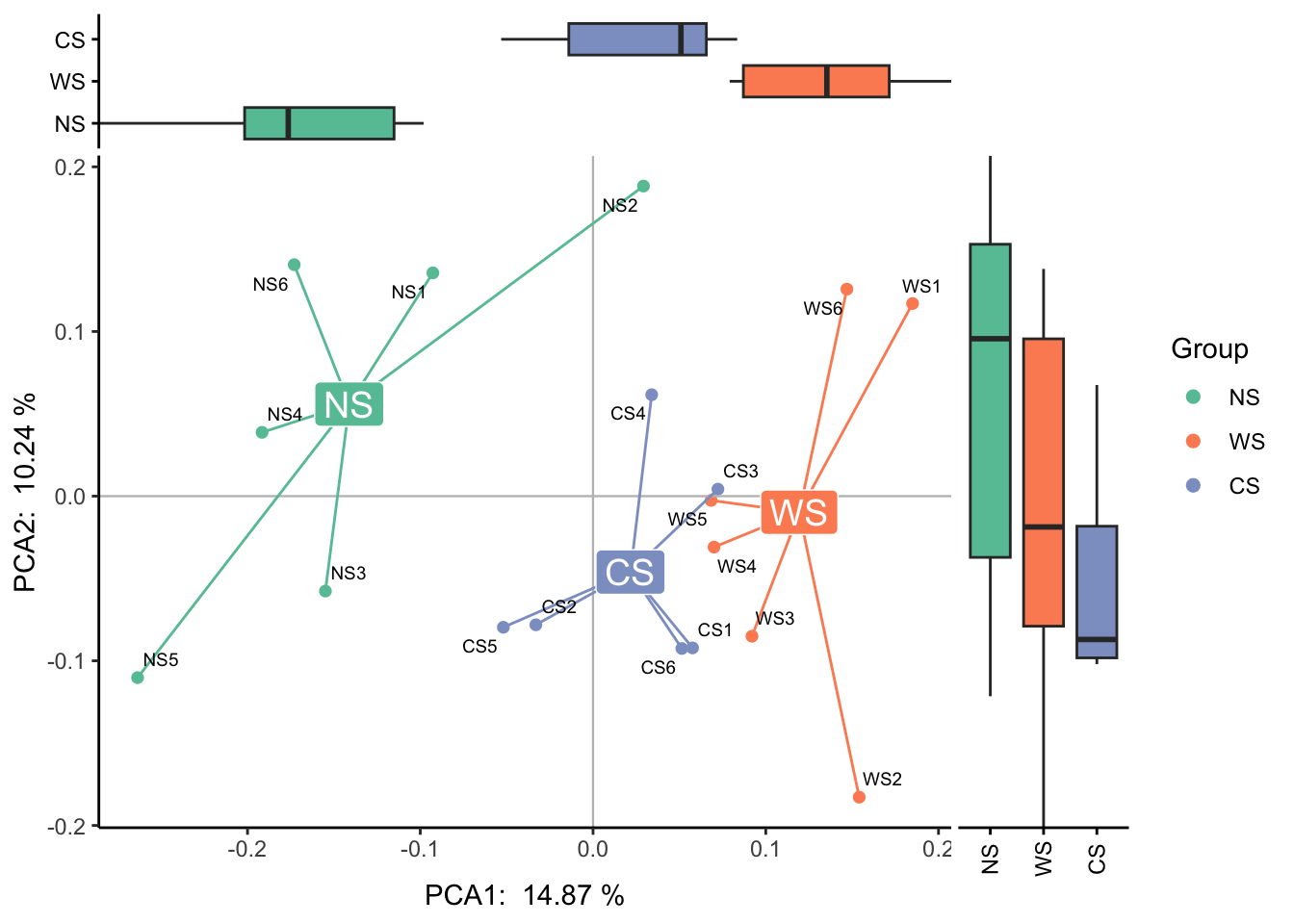
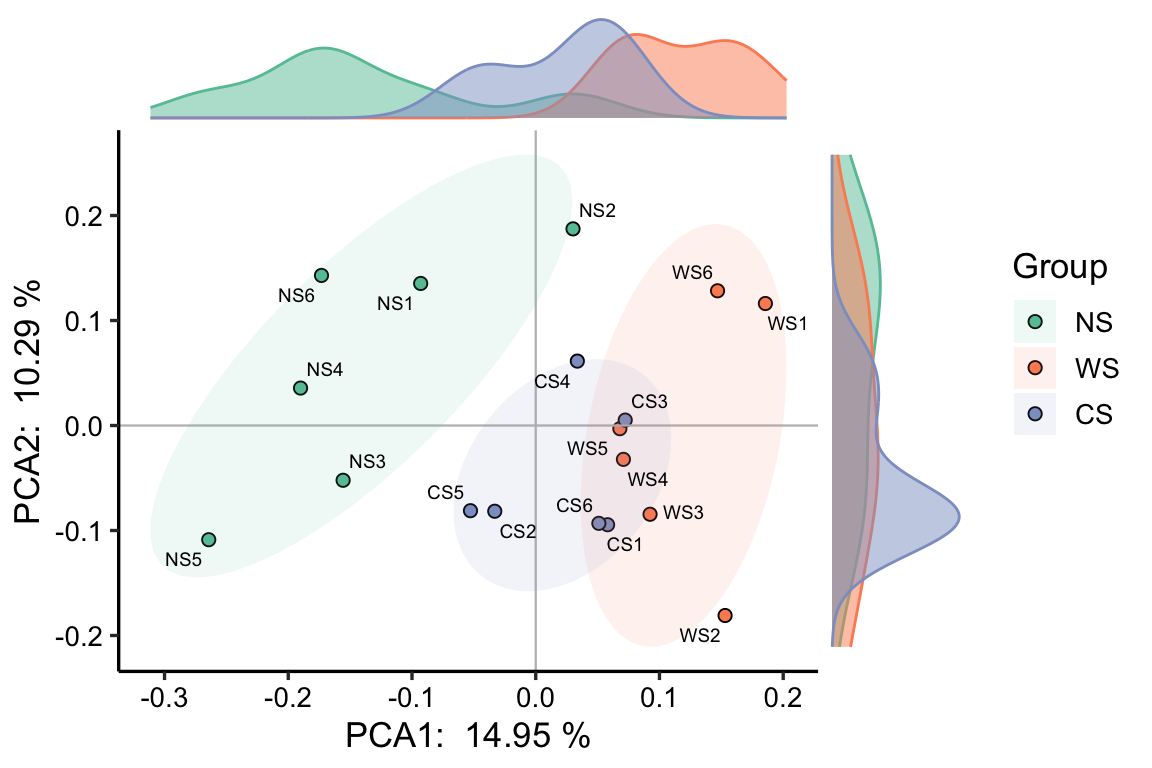
margin 可以画出点的分布密度图或箱形图:

1

plot(b_res,Group = "Group",metadata = metadata,margin = T,mode = 3)

## $PCA

1

plot(b_res,Group = "Group",metadata = metadata,margin = T,box = F)

## $PCA

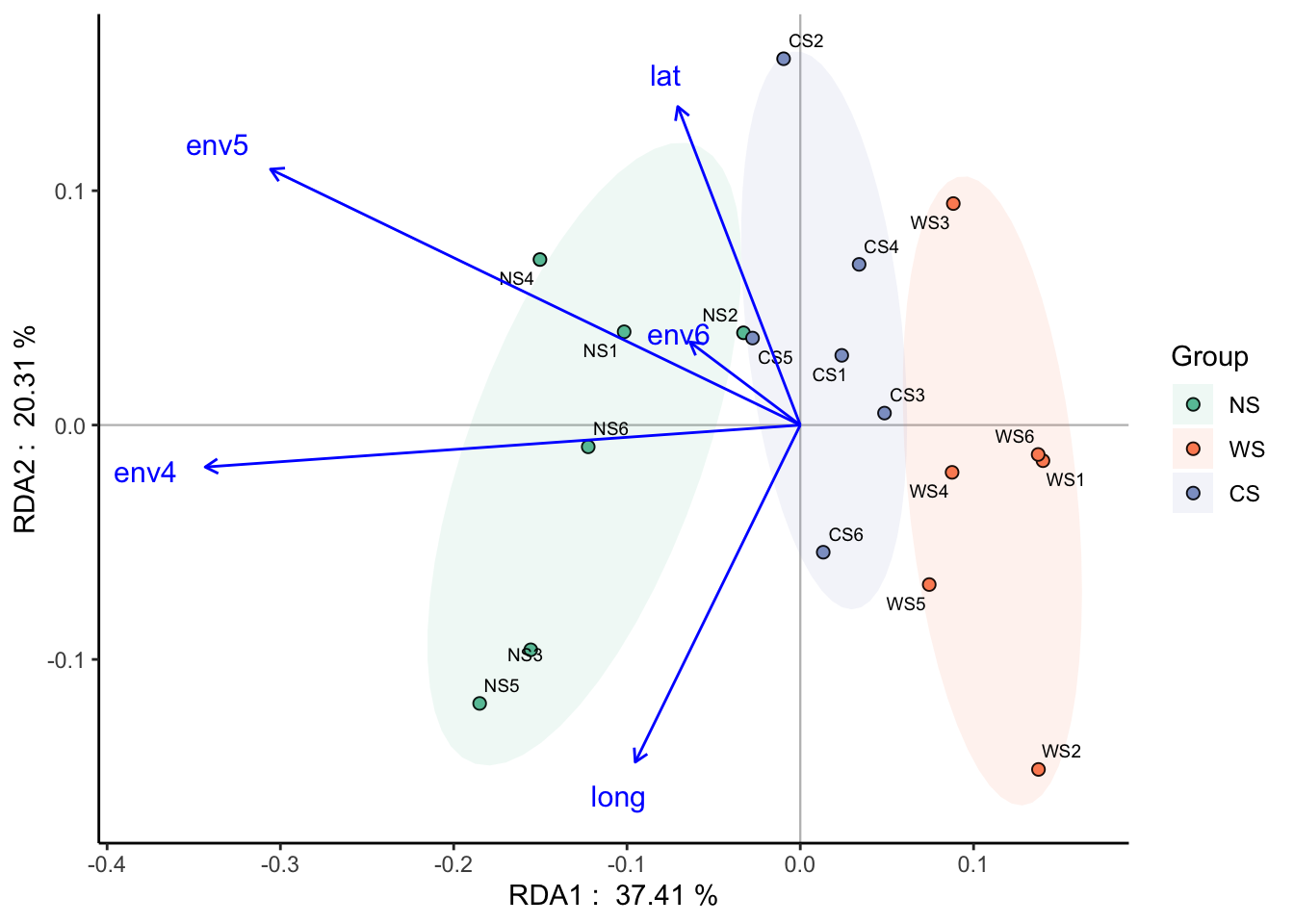
限制性排序则需要输入响应变量数据和我们要研究的环境数据：

以RDA分析为例：

1
2
3
4


data(otutab,package = "pcutils")
env=metadata[,6:10]
#RDA
myRDA(otutab,env)->phy.rda

## 
## Call:
## vegan::decorana(veg = dat.h) 
## 
## Detrended correspondence analysis with 26 segments.
## Rescaling of axes with 4 iterations.
## Total inertia (scaled Chi-square): 0.3207 
## 
##                         DCA1    DCA2    DCA3    DCA4
## Eigenvalues          0.03127 0.02265 0.01916 0.01729
## Additive Eigenvalues 0.03127 0.02265 0.01917 0.01727
## Decorana values      0.03150 0.02146 0.01701 0.01035
## Axis lengths         0.74268 0.74498 0.57253 0.52361
## 
## DCA analysis, select the sorting analysis model according to the first value of the Axis lengths row
##    Axis Lengths >4.0-CCA (based on unimodal model, canonical correspondence analysis);
##    If it is between 3.0-4.0 - both RDA/CCA;
##    If less than 3.0-RDA (based on linear model, redundancy analysis)
## [1] "===============Initial Model================"
## [1] "Initial cca, vif>20 indicates serious collinearity:"
##     env4     env5     env6      lat     long 
## 2.671744 3.148860 1.161378 1.417139 1.120735 
## Initial Model R-square: 0.05504835 
## [1] "=============Statistics==========="
## 0.3329753 Constrained indicates the degree to which environmental factors explain differences in community structure
## 0.6670247 unconstrained means that the environmental factors cannot explain the part of the community structure

1

RDA_plot(phy.rda,"Group",metadata)

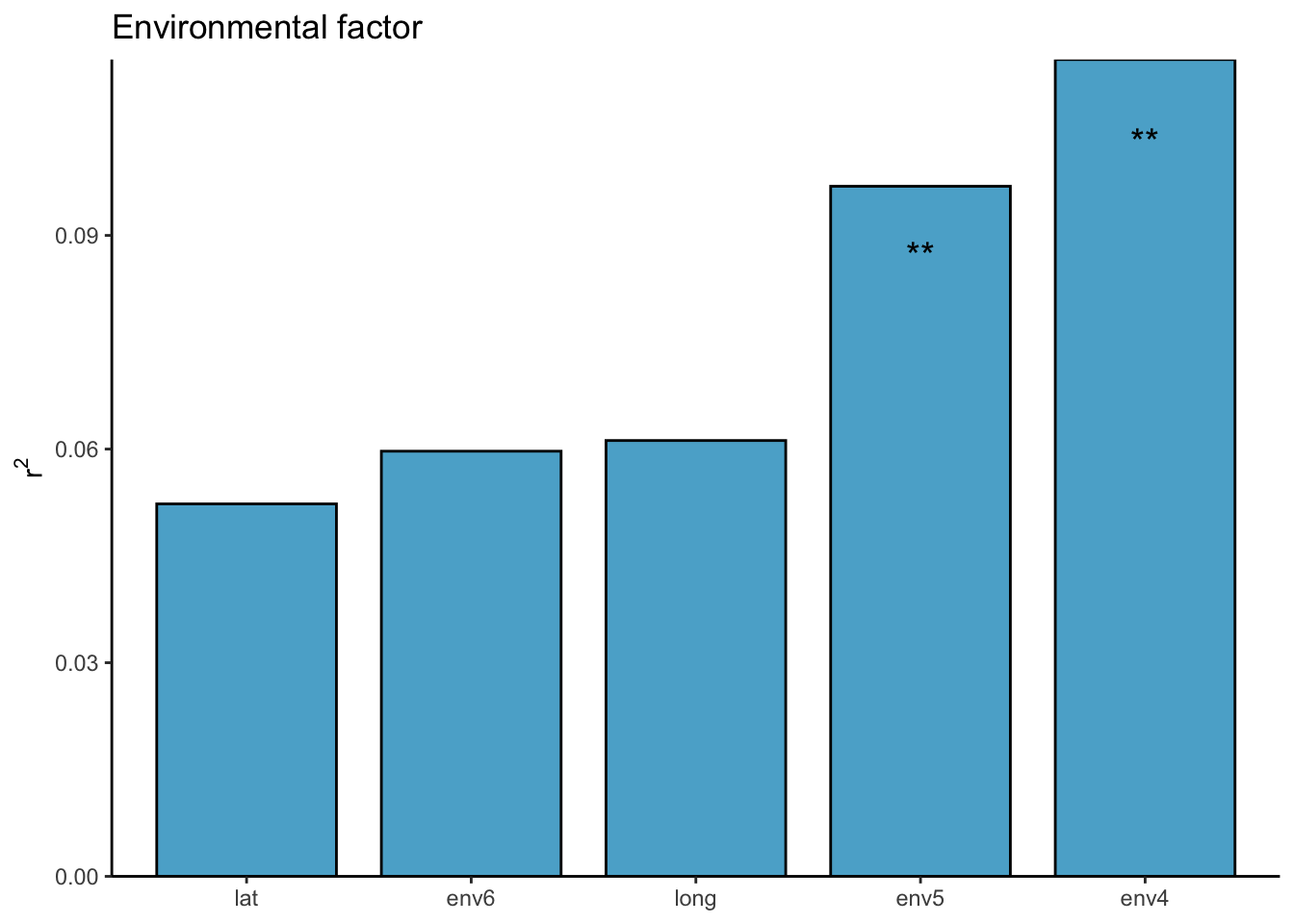
对于这里每一个环境因素的检验，我们仍然可以使用adonis，或者envfit，bioenv等检验方式：

1
2


adonis_res=pctax::permanova(otutab,env,method = "adonis")
plot(adonis_res)

1
2


envfit_res=pctax::envfitt(phy.rda,env)
plot(envfit_res,mode=1)

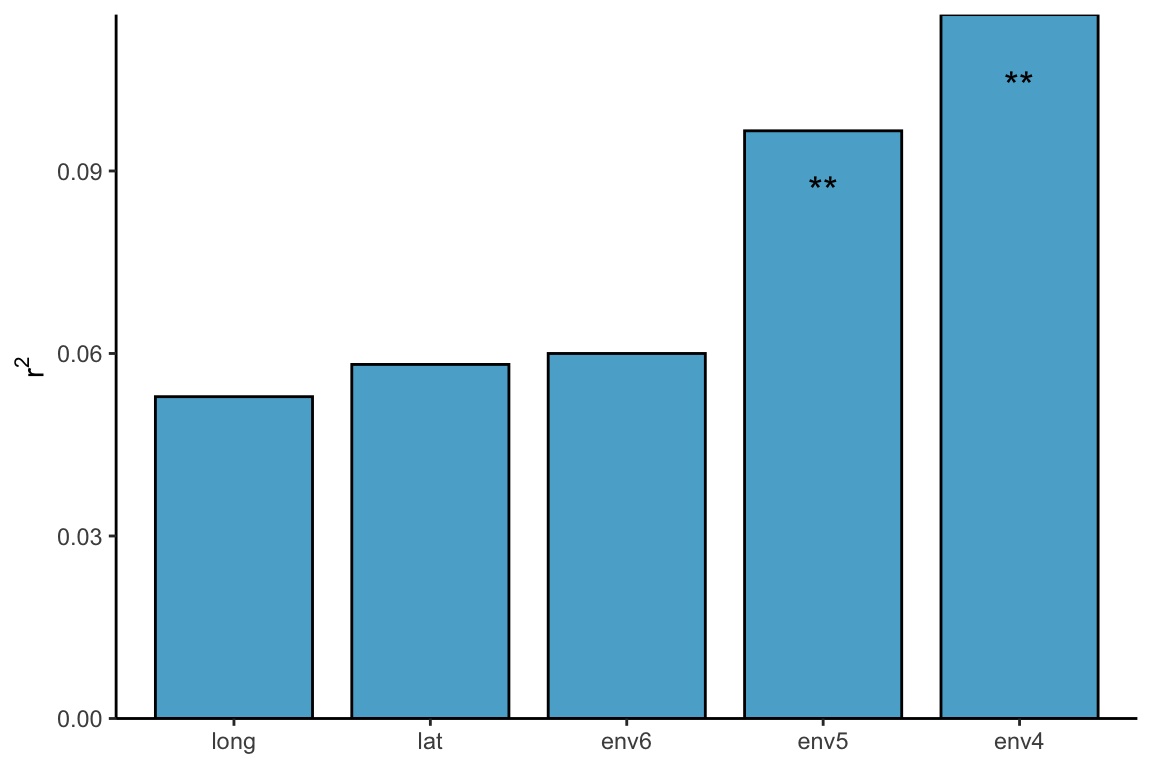
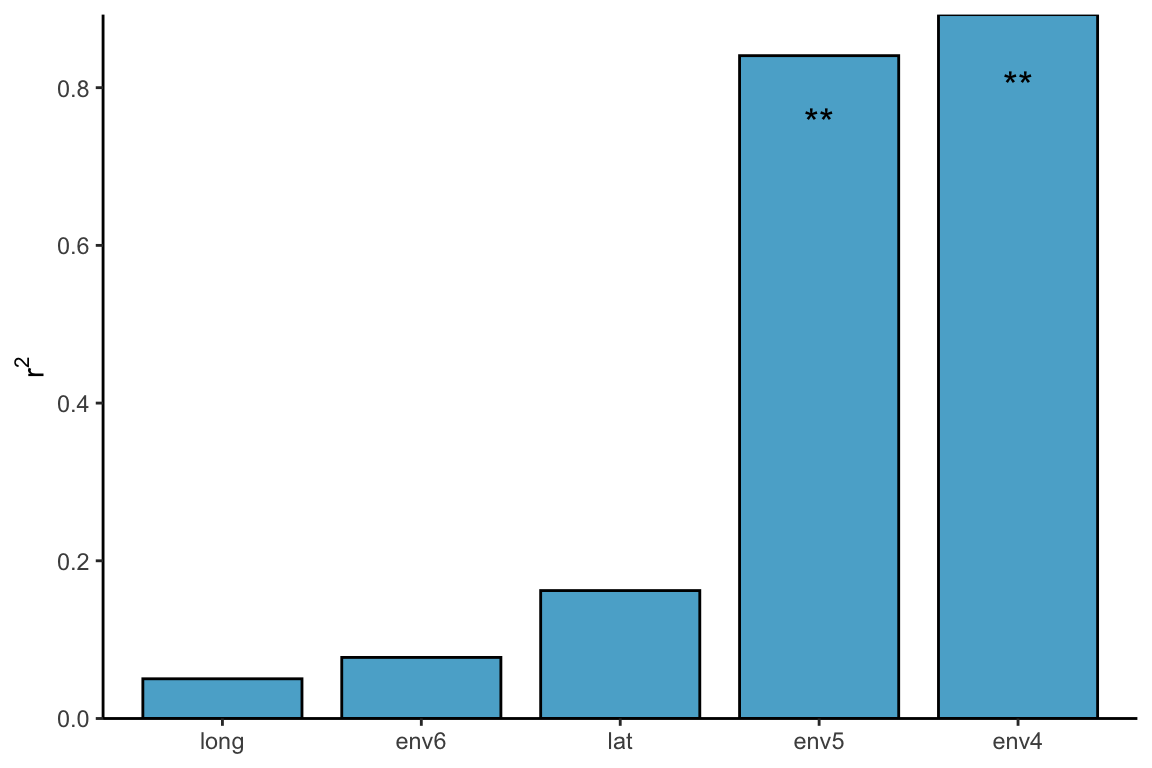
限制性排序比较复杂，如果输入的环境因素较多具有共线性，还应该对得到的结果使用ordistep进行forward，backward，both等方式的筛选，得到最合适的模型。